Difference between revisions of "CoE Cluster April 2012"
m (→Results) |
m (→CUDA Code Listing) |
||
| (36 intermediate revisions by 2 users not shown) | |||
| Line 2: | Line 2: | ||
=Assignments= | =Assignments= | ||
| − | *[[/ | + | *[[CoE_Cluster_november_2011/MD5_attack_singlethreaded|MD5 attack singlethreaded]] |
| − | *[[ | + | *[[CoE_Cluster_november_2011/MPI|Programmering med MPI]] |
| − | + | ||
| − | |||
=Results= | =Results= | ||
| + | Having investigated CUDA C programming for Nvidia graphics cards and the CUDA architecture, we made some performance measurements using a range of numbers of blocks and threads, executing in parallel. The test program calculated values of the [http://en.wikipedia.org/wiki/Mandelbrot_set Mandelbrot Set ] on a pixel-by-pixel basis. The Mandelbrot Set was a good choice for this test beacuse: | ||
| + | * It is relatively easy to program (see code listing below) | ||
| + | * Every pixel has to calculated individually - there is no correlation between values of neighbouring pixels | ||
| + | * The image can be separated into parts which can be calculated separately and in parallel | ||
| + | * The time taken to calculate a complete image without parallelization is long enough to allow the performance gains from parallelization to be clearly seen | ||
| + | * The resulting images are very pretty (if a little strange)! :-) | ||
| + | |||
| + | The results of the benchmarking are here, as an interactive chart (hover your mouse to find out which values are represented by each line, drag to zoom and hide/reveal curves relating to the number of blocks in the legend beneath): | ||
| + | |||
| + | *[http://mars.tekkom.dk/js/cuda_benchmark.htm CUDA Benchmark] (External JavaScript) | ||
| + | |||
| + | Along with the CUDA C programming Guide (see Literature List), the [http://developer.download.nvidia.com/compute/cuda/CUDA_Occupancy_calculator.xls CUDA Occupancy Calculator] provides a good basis for understanding and explaining the results seen. In general, it was found that more than 32 blocks and/or 128 threads per block did not provide noticable performance gains, whereas there were significant performance gains for every step increase below these values. This independent presentation: [[Media:cuda_presentation.ppt]] provides a comprehensive explanation and confirmation of the results we obtained. | ||
| + | |||
| + | [[File:cuda_mandelbrot.png]] | ||
| + | |||
| + | ''Above: Mandelbrot Set drawn in 0,12 seconds, using a single NVidia CUDA capable graphics card (GeForce GTX 460) running 32 blocks and 128 threads in each block. Total image dimension 512 x 512 pixels.'' | ||
| + | |||
| + | For the reasons given above, the Mandelbrot Set was also a good candidate for testing [http://en.wikipedia.org/wiki/Message_Passing_Interface Message Passing Interface - MPI] programming capabilities and strategies. To support graphical output, the final program used a "Master" process which collected calculated values from "Worker" processes and set them together in an X Window. This was a good illustration of the idea that some processes, like Input-Output, have to be run in a serial manner and that perfect parallelization is rarely achievable in practice c.f. [http://en.wikipedia.org/wiki/Amdahl%27s_law Amdahl's Law] | ||
| + | |||
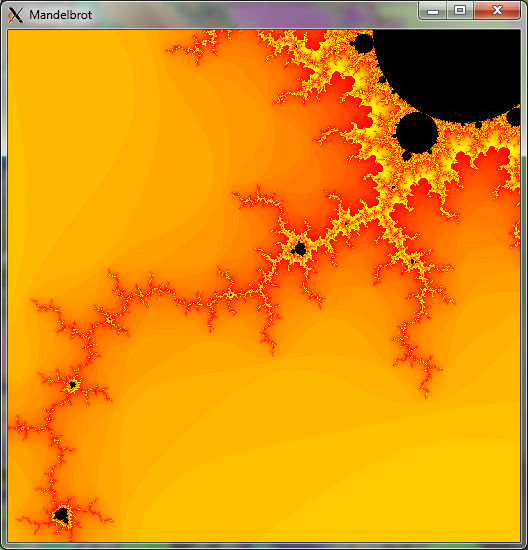
[[File:mpi_mandelbrot.png]] | [[File:mpi_mandelbrot.png]] | ||
| − | Mandelbrot Set drawn in 1,2 seconds, using a Master-Worker MPI pattern with 16 worker nodes and 1 master node (which collected calculated results from different parts of the image and output them to an X Window). Total image dimension 800 x 800 pixels. | + | ''Above: Mandelbrot Set drawn in 1,2 seconds, using a Master-Worker MPI pattern with 16 worker nodes and 1 master node (which collected calculated results from different parts of the image and output them to an X Window). Total image dimension 800 x 800 pixels.'' |
| + | |||
| + | =CUDA Code Listing= | ||
| − | + | <source lang=c> | |
| + | |||
| + | // mandelbrot.cu | ||
| + | |||
| + | // Calculate number of iterations required to make each point | ||
| + | // in Mandelbrot Set diverge and colour the corresponding pixel | ||
| + | // Tends to work faster with floats rather than doubles - but | ||
| + | // at the expense of "colour blocking" at lower resolutions | ||
| + | |||
| + | // Paul Saunders | ||
| + | // Mercantec | ||
| + | // 03/11-2011 | ||
| + | |||
| + | //#include <stdio.h> | ||
| + | //#include <stdlib.h> | ||
| + | //#include <unistd.h> | ||
| + | |||
| + | __device__ inline int calcMandelbrot(const double xPos, const double yPos, const int crunch) | ||
| + | { | ||
| + | double y = yPos; | ||
| + | double x = xPos; | ||
| + | double yy = y * y; | ||
| + | double xx = x * x; | ||
| + | int i = crunch; | ||
| + | |||
| + | while (--i && (xx + yy < 4.0f)) { | ||
| + | y = x * y * 2.0f + yPos; | ||
| + | x = xx - yy + xPos; | ||
| + | yy = y * y; | ||
| + | xx = x * x; | ||
| + | } | ||
| + | return i; | ||
| + | } // CalcMandelbrot - count down until iterations are used up or until the calculation diverges | ||
| + | |||
| + | __device__ void RGB(int x, int y, unsigned char* m, int step, int iter_count) | ||
| + | { | ||
| + | unsigned char *p; | ||
| + | unsigned int rgb; | ||
| + | p = ((unsigned char *) (m + step*x)+3*y); | ||
| + | rgb = *p+((*(p+1))<<8)+((*(p+2))<<16); | ||
| + | |||
| + | rgb = iter_count*2048; | ||
| + | |||
| + | *p = (unsigned char) (rgb&0xff); | ||
| + | *(p+1) = (unsigned char) ((rgb>>8)&0xff); | ||
| + | *(p+2) = (unsigned char) ((rgb>>16)&0xff); | ||
| + | return; | ||
| + | } //Use calculated iteration count to determine the colour for each pixel | ||
| − | + | __global__ void Count(unsigned char *img, int rows, int cols, int step, int max_iterations, double centre_x, | |
| + | double centre_y, double size, int image_size) | ||
| + | { | ||
| + | double rowfac = ((double) rows)/gridDim.x; | ||
| + | int rowstart = blockIdx.x*rowfac; | ||
| + | int rowend = (blockIdx.x+1)*rowfac; | ||
| + | double colfac = ((double) cols)/blockDim.x; | ||
| + | int colstart = threadIdx.x*colfac; | ||
| + | int colend = (threadIdx.x+1)*colfac; | ||
| + | |||
| + | double left_edge = centre_x - size/2.0; | ||
| + | double top_edge = centre_y - size/2.0; | ||
| + | double pixel_step = size/image_size; | ||
| + | |||
| + | for (int i=rowstart; i<rowend; i++) | ||
| + | { | ||
| + | for (int j=colstart; j<colend; j++) | ||
| + | { | ||
| + | RGB(i, j, img, step, calcMandelbrot(left_edge + j * pixel_step, top_edge + i * pixel_step, max_iterations)); | ||
| + | } | ||
| + | } | ||
| + | } //Divide calculations between the requested number of blocks and threads, having used the matrix's geometry to | ||
| + | //determine the values input to the calculation for each pixel | ||
| − | + | void startCUDA(int blocks, int threads, int iterations, double centre_x, double centre_y, | |
| + | double size, unsigned char* img, int rows, int cols, int step, int image_size) | ||
| + | { | ||
| + | if (img!=NULL) | ||
| + | { | ||
| + | dim3 dimBlock(threads, 1, 1); | ||
| + | dim3 dimGrid(blocks, 1, 1); | ||
| + | |||
| + | unsigned char *CUDAimg; | ||
| + | cudaMalloc((void**) &CUDAimg, rows*cols*3); | ||
| + | cudaMemcpy(CUDAimg, img, rows*cols*3, cudaMemcpyHostToDevice); | ||
| + | Count<<<dimGrid, dimBlock>>>(CUDAimg, rows, cols, step, iterations, centre_x, centre_y, size, image_size); | ||
| + | cudaMemcpy(img, CUDAimg, rows*cols*3, cudaMemcpyDeviceToHost); | ||
| + | cudaFree(CUDAimg); | ||
| + | } | ||
| + | } // Allocate sufficient memory for the whole image (@3 bytes per pixel), | ||
| + | //transfer it to the graphics card (host to device), start the calculation process and, | ||
| + | //when complete, transfer the memory (containing the calculated values) back to the host | ||
| + | </source> | ||
=Slides= | =Slides= | ||
Latest revision as of 08:11, 2 May 2012
{{#img: image=Super-computer-artw.jpg | page=Linux Cluster til Center of Excelence/Beskrivelse til CoE West | width=200px | title=Linux Supercomputer projekt }}
Assignments
Results
Having investigated CUDA C programming for Nvidia graphics cards and the CUDA architecture, we made some performance measurements using a range of numbers of blocks and threads, executing in parallel. The test program calculated values of the Mandelbrot Set on a pixel-by-pixel basis. The Mandelbrot Set was a good choice for this test beacuse:
- It is relatively easy to program (see code listing below)
- Every pixel has to calculated individually - there is no correlation between values of neighbouring pixels
- The image can be separated into parts which can be calculated separately and in parallel
- The time taken to calculate a complete image without parallelization is long enough to allow the performance gains from parallelization to be clearly seen
- The resulting images are very pretty (if a little strange)! :-)
The results of the benchmarking are here, as an interactive chart (hover your mouse to find out which values are represented by each line, drag to zoom and hide/reveal curves relating to the number of blocks in the legend beneath):
- CUDA Benchmark (External JavaScript)
Along with the CUDA C programming Guide (see Literature List), the CUDA Occupancy Calculator provides a good basis for understanding and explaining the results seen. In general, it was found that more than 32 blocks and/or 128 threads per block did not provide noticable performance gains, whereas there were significant performance gains for every step increase below these values. This independent presentation: Media:cuda_presentation.ppt provides a comprehensive explanation and confirmation of the results we obtained.
Above: Mandelbrot Set drawn in 0,12 seconds, using a single NVidia CUDA capable graphics card (GeForce GTX 460) running 32 blocks and 128 threads in each block. Total image dimension 512 x 512 pixels.
For the reasons given above, the Mandelbrot Set was also a good candidate for testing Message Passing Interface - MPI programming capabilities and strategies. To support graphical output, the final program used a "Master" process which collected calculated values from "Worker" processes and set them together in an X Window. This was a good illustration of the idea that some processes, like Input-Output, have to be run in a serial manner and that perfect parallelization is rarely achievable in practice c.f. Amdahl's Law
Above: Mandelbrot Set drawn in 1,2 seconds, using a Master-Worker MPI pattern with 16 worker nodes and 1 master node (which collected calculated results from different parts of the image and output them to an X Window). Total image dimension 800 x 800 pixels.
CUDA Code Listing
// mandelbrot.cu
// Calculate number of iterations required to make each point
// in Mandelbrot Set diverge and colour the corresponding pixel
// Tends to work faster with floats rather than doubles - but
// at the expense of "colour blocking" at lower resolutions
// Paul Saunders
// Mercantec
// 03/11-2011
//#include <stdio.h>
//#include <stdlib.h>
//#include <unistd.h>
__device__ inline int calcMandelbrot(const double xPos, const double yPos, const int crunch)
{
double y = yPos;
double x = xPos;
double yy = y * y;
double xx = x * x;
int i = crunch;
while (--i && (xx + yy < 4.0f)) {
y = x * y * 2.0f + yPos;
x = xx - yy + xPos;
yy = y * y;
xx = x * x;
}
return i;
} // CalcMandelbrot - count down until iterations are used up or until the calculation diverges
__device__ void RGB(int x, int y, unsigned char* m, int step, int iter_count)
{
unsigned char *p;
unsigned int rgb;
p = ((unsigned char *) (m + step*x)+3*y);
rgb = *p+((*(p+1))<<8)+((*(p+2))<<16);
rgb = iter_count*2048;
*p = (unsigned char) (rgb&0xff);
*(p+1) = (unsigned char) ((rgb>>8)&0xff);
*(p+2) = (unsigned char) ((rgb>>16)&0xff);
return;
} //Use calculated iteration count to determine the colour for each pixel
__global__ void Count(unsigned char *img, int rows, int cols, int step, int max_iterations, double centre_x,
double centre_y, double size, int image_size)
{
double rowfac = ((double) rows)/gridDim.x;
int rowstart = blockIdx.x*rowfac;
int rowend = (blockIdx.x+1)*rowfac;
double colfac = ((double) cols)/blockDim.x;
int colstart = threadIdx.x*colfac;
int colend = (threadIdx.x+1)*colfac;
double left_edge = centre_x - size/2.0;
double top_edge = centre_y - size/2.0;
double pixel_step = size/image_size;
for (int i=rowstart; i<rowend; i++)
{
for (int j=colstart; j<colend; j++)
{
RGB(i, j, img, step, calcMandelbrot(left_edge + j * pixel_step, top_edge + i * pixel_step, max_iterations));
}
}
} //Divide calculations between the requested number of blocks and threads, having used the matrix's geometry to
//determine the values input to the calculation for each pixel
void startCUDA(int blocks, int threads, int iterations, double centre_x, double centre_y,
double size, unsigned char* img, int rows, int cols, int step, int image_size)
{
if (img!=NULL)
{
dim3 dimBlock(threads, 1, 1);
dim3 dimGrid(blocks, 1, 1);
unsigned char *CUDAimg;
cudaMalloc((void**) &CUDAimg, rows*cols*3);
cudaMemcpy(CUDAimg, img, rows*cols*3, cudaMemcpyHostToDevice);
Count<<<dimGrid, dimBlock>>>(CUDAimg, rows, cols, step, iterations, centre_x, centre_y, size, image_size);
cudaMemcpy(img, CUDAimg, rows*cols*3, cudaMemcpyDeviceToHost);
cudaFree(CUDAimg);
}
} // Allocate sufficient memory for the whole image (@3 bytes per pixel),
//transfer it to the graphics card (host to device), start the calculation process and,
//when complete, transfer the memory (containing the calculated values) back to the host
Slides
Litteratur Liste
- MPI
- Introduction to Parallel Computing
- CUDA Overview from Nvidia
- Nvidia CUDA C Programming Guide
- OpenCV Tutorial
- OpenCV Reference
- Skin Detection algorithms for use in OpenCV/CUDA trials