Revision as of 08:44, 1 May 2012

{{#img: image=Super-computer-artw.jpg | page=Linux Cluster til Center of Excelence/Beskrivelse til CoE West | width=200px | title=Linux Supercomputer projekt }}

Assignments

Results

Having investigated CUDA C programming for Nvidia graphics cards and the CUDA architecture, we made some performance measurements using a range of numbers of blocks and threads, executing in parallel. The test program calculated values of the Mandelbrot Set on a pixel-by-pixel basis. The Mandelbrot Set was a good choice for this test beacuse:

It is relatively easy to program
Every pixel has to calculated individually - there is no correlation between values of neighbouring pixels
The image can be separated into parts which can be calculated separately and in parallel
The time taken to calculate a complete image without parallelization is long enough to allow the performance gains from parallelization to be clearly seen
The resulting images are very pretty (if a little strange)! :-)

The results of the benchmarking are here, as an interactive chart (hover your mouse to find out which values are represented by each line, drag to zoom and hide/reveal curves relating to the number of blocks in the legend beneath):

CUDA Benchmark (External JavaScript)

Along with the CUDA C programming Guide (see Literature List), the CUDA Occupancy Calculator provides a good basis for understanding and explaining the results seen. In general, it was found that more than 32 blocks and/or 128 threads per block did not provide noticable performance gains, whereas there were significant performance gains for every step increase below these values.

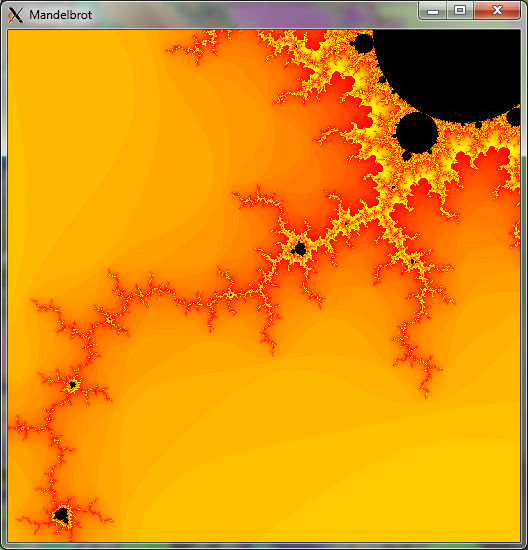
Above: Mandelbrot Set drawn in 0,12 seconds, using a single NVidia CUDA capable graphics card (GeForce GTX 460) running 32 blocks and 128 threads in each block. Total image dimension 512 x 512 pixels.

For the reasons given above, the Mandelbrot Set was also a good candidate for testing Message Passing Interface - MPI programming capabilities and strategies. To support graphical output, the final program used a "Master" process which collected calculated values from "Worker" processes and set them together in an X Window. This was a good illustration of the idea that some processes, like Input-Output, have to be run in a serial manner and that perfect parallelization is rarely achievable in practice c.f. Amdahl's Law

Above: Mandelbrot Set drawn in 1,2 seconds, using a Master-Worker MPI pattern with 16 worker nodes and 1 master node (which collected calculated results from different parts of the image and output them to an X Window). Total image dimension 800 x 800 pixels.

Code Listing

// mandelbrot.cu

// Calculate number of iterations required to make each point in Mandelbrot Set diverge and colour the corresponding pixel // Tends to work faster with floats rather than doubles - but at the expense of "colour blocking" at lower resolutions

// Paul Saunders // Mercantec // 03/11-2011

//#include <stdio.h> //#include <stdlib.h> //#include <unistd.h>

__device__ inline int calcMandelbrot(const double xPos, const double yPos, const int crunch) {

   double y = yPos;
   double x = xPos;
   double yy = y * y;
   double xx = x * x;
   int i = crunch;

   while (--i && (xx + yy < 4.0f)) {
       y = x * y * 2.0f + yPos;
       x = xx - yy + xPos;
       yy = y * y;
       xx = x * x;
   }
   return i;

} // CalcMandelbrot - count down until iterations are used up or until the calculation diverges

__device__ void RGB(int x, int y, unsigned char* m, int step, int iter_count) {

 unsigned char *p;
 unsigned int rgb;
 p = ((unsigned char *) (m + step*x)+3*y);
 rgb = *p+((*(p+1))<<8)+((*(p+2))<<16);
 
 rgb = iter_count*2048;
 
 *p = (unsigned char) (rgb&0xff);
 *(p+1) = (unsigned char) ((rgb>>8)&0xff);
 *(p+2) = (unsigned char) ((rgb>>16)&0xff);
 return;

} //Use calculated iteration count to determine the colour for each pixel

__global__ void Count(unsigned char *img, int rows, int cols, int step, int max_iterations, double centre_x, double centre_y, double size, int image_size) {

 double rowfac = ((double) rows)/gridDim.x;
 int rowstart = blockIdx.x*rowfac;
 int rowend = (blockIdx.x+1)*rowfac;
 double colfac = ((double) cols)/blockDim.x;
 int colstart = threadIdx.x*colfac;
 int colend = (threadIdx.x+1)*colfac;
 
 double left_edge = centre_x - size/2.0;
 double top_edge = centre_y - size/2.0;
 double pixel_step = size/image_size;
 
 for (int i=rowstart; i<rowend; i++)
   {
     for (int j=colstart; j<colend; j++)
     {
       RGB(i, j, img, step, calcMandelbrot(left_edge + j * pixel_step, top_edge + i * pixel_step, max_iterations));
     }
   }

} //Divide calculations between the requested number of blocks and threads, having used the matrix's geometry to determine the values input to the calculation for each pixel

void startCUDA(int blocks, int threads, int iterations, double centre_x, double centre_y, double size, unsigned char* img, int rows, int cols, int step, int image_size) {

  if (img!=NULL)
  {
     dim3 dimBlock(threads, 1, 1);

dim3 dimGrid(blocks, 1, 1);

     unsigned char *CUDAimg;
     cudaMalloc((void**) &CUDAimg, rows*cols*3);
     cudaMemcpy(CUDAimg, img, rows*cols*3, cudaMemcpyHostToDevice);
     Count<<<dimGrid, dimBlock>>>(CUDAimg, rows, cols, step, iterations, centre_x, centre_y, size, image_size);
     cudaMemcpy(img, CUDAimg, rows*cols*3, cudaMemcpyDeviceToHost);
     cudaFree(CUDAimg);
  }

} // Allocate sufficient memory for the whole image (@3 bytes per pixel), transfer it to the graphics card (host to device), start the calculation process and, when complete, transfer the memory (containing the calculated values) back to the host </source lang=c>

Slides

Litteratur Liste

Evaluering

Navigation menu

Difference between revisions of "CoE Cluster April 2012"