Difference between revisions of "Enigma/primer"
m |
m |
||
| Line 1: | Line 1: | ||
| + | {{TOCright}} | ||
| + | {| | ||
| + | |[[Image:Enigma6.gif|300px]][[Image:Enigma2.jpg|130px|right]] | ||
| + | |} | ||
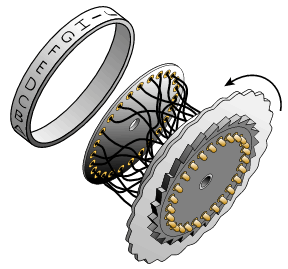
=The Wheels= | =The Wheels= | ||
The Wheels can be installed in the Enigma in any sequence. If there are five different Wheels in total and the Enigma uses three Wheels. The total number of Wheel combinatins would be <math>5*4*3=60</math> | The Wheels can be installed in the Enigma in any sequence. If there are five different Wheels in total and the Enigma uses three Wheels. The total number of Wheel combinatins would be <math>5*4*3=60</math> | ||
Revision as of 19:03, 6 December 2010
|
The Wheels
The Wheels can be installed in the Enigma in any sequence. If there are five different Wheels in total and the Enigma uses three Wheels. The total number of Wheel combinatins would be <math>5*4*3=60</math>
The software enigma
In the software Enigma you would need some random Wheels and a Random Rotor Reftlector. For examle this three bit Enigma.
Three bit Example
Crypt
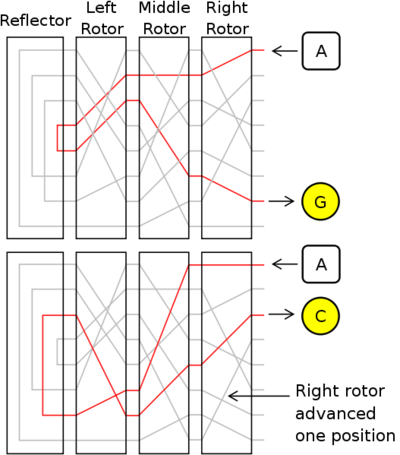
In the example below if the input=2 its send to Wheel 1 position 2 which output will be 1 and that's input for Wheel 2 which outputs 0 to the Reflector that outputs 7 as input for Reverse Wheel 2 which output's 2 as input for Reverse wheel 1 which Output 0 as the encrypted message.
- 2->1->0->7->2->0
Input 0, 1, <notice>2</notice>, 3, 4, 5, 6, 7
Wheel 1 2, 7, <notice>1</notice>, 5, 6, 3, 0, 4
Wheel 2 5, <notice>0</notice>, 7, 2, 1, 6, 4, 3
Reflector <notice>7</notice>, 4, 6, 5, 1, 3, 2, 0
Reverse wheel 2 1, 4, 3, 7, 6, 0, 5, <notice>2</notice>
Reverse wheel 1(output) 6, 2, <notice>0</notice>, 5, 7, 3, 4, 1Decrypt
- Reverse: 0->2->7->0->1->2
Input <notice>0</notice>, 1, 2, 3, 4, 5, 6, 7
Wheel 1 <notice>2</notice>, 7, 1, 5, 6, 3, 0, 4
Wheel 2 5, 0, <notice>7</notice>, 2, 1, 6, 4, 3
Reflector 7, 4, 6, 5, 1, 3, 2, <notice>0</notice>
Reverse wheel 2 <notice>1</notice>, 4, 3, 7, 6, 0, 5, 2
Reverse wheel 1(output) 6, <notice>2</notice>, 0, 5, 7, 3, 4, 1The wheel notch
Each time a letter/digit is encrypted/decrypted - same process - the Wheels are ticked forward.
Tick 1
Wheel 1 is ticked forward on every encryption/decryption. See below. When the Notch - show in red below - ticks from 7 to 0 it will Tick the next Wheel. See Tick 2.
| Wheel positions before Tick number 1 |
Input 0, 1, 2, 3, 4, 5, 6, 7
Wheel 1 <notice>2, 7, 1, 5, 6, 3, <error>0</error>, 4</notice>
Wheel 2 5, 0, 7, 2, 1, 6, <error>4,</error> 3
Reflector 7, 4, 6, 5, 1, 3, 2, 0
Reverse wheel 2 <notice>1, 4, 3, 7, 6, 0, 5, 2</notice>
Reverse wheel 1(output) 6, 2, 0, 5, 7, 3, 4, 1 |
| Wheel positions after Tick number 1 |
Input 0, 1, 2, 3, 4, 5, 6, 7
Wheel 1 <notice>4, 2, 7, 1, 5, 6, 3, <error>0</error></notice>
Wheel 2 5, 0, 7, 2, 1, 6, <error>4</error>, 3
Reflector 7, 4, 6, 5, 1, 3, 2, 0
Reverse wheel 2 1, 4, 3, 7, 6, 0, 5, 2
Reverse wheel 1(output) <notice>2, 0, 5, 7, 3, 4, 1, 6</notice> |
Tick 2
Wheel 1's Notch is ticked from 7 to 0 it will Tick wheel 2 forward. The reflector will stay stationary.
| Wheel positions before Tick number 2 | |
Input 0, 1, 2, 3, 4, 5, 6, 7
Wheel 1 <notice>4, 2, 7, 1, 5, 6, 3, <error>0</error></notice>
Wheel 2 5, 0, 7, 2, 1, 6, <error>4</error>, 3
Reflector 7, 4, 6, 5, 1, 3, 2, 0
Reverse wheel 2 1, 4, 3, 7, 6, 0, 5, 2
Reverse wheel 1(output) <notice>2, 0, 5, 7, 3, 4, 1, 6</notice> | |
| Wheel positions after Tick number 2 | |
Input 0, 1, 2, 3, 4, 5, 6, 7
Wheel 1 <notice><error>0</error>, 4, 2, 7, 1, 5, 6, 3</notice>
Wheel 2 <notice>3, 5, 0, 7, 2, 1, 6, <error>4</error></notice>
Reflector 7, 4, 6, 5, 1, 3, 2, 0
Reverse wheel 2 <notice>2, 1, 4, 3, 7, 6, 0, 5</notice>
Reverse wheel 1(output) <notice>6, 2, 0, 5, 7, 3, 4, 1</notice>Crypto strength of three bit EnigmaIf the Wheels and Reflector are known to the hacker
If the Wheels and Reflector are unknown to the hacker
Not that impressive, see the 8 bit example below 8 bit exampleNumber of possible keys when using three wheelsIn the example below there is a caculation of possible keys that is
If we used a 10 bit rotorOr try and imagine a 32 bit wheel (Then we would need a better implementation of frac) <notice>frac(1024)</notice>
54185287960588572830769219446838547380015539635380134444828702706832\
10612073376603733140984136214586719079188457089807539319941657701873\
68260454133333721939108367528012764993769768292516937891165755680659\
66374794731451840488667767255612518869433525121367727452196343077013\
37132057962484331288700884361716546902375183904529447322778084029321\
58722061853806162806063925435310822186848239287130261690914211362251\
14468471388858788162925210404629531594994390035788241024393431503744\
41138908061814062108639532752353758850185984515822295996545585412427\
89130902486944298610923153307579131675745146436304024890820442907734\
56182736903050225279692655307296737099075874779312763510470246988966\
79614621330262371589732278578146318071564277676440645910850765647834\
56324457736853810336981776080498707767046394272605341416779125697733\
37456803747518667626596166561588468145026333704252266414186215704682\
56847733609443267374936766749150989537681129458316266438564790278163\
85730291542667725665642276826058264393884514911976419675509290208592\
71315636298329098944105273212518724952750131407167640551693619078182\
12367019122957673631170541265899299164820085157817519554669109028387\
29232224509906388638147771255227782631322385756948819393658889908993\
67087451686065309841102029985381628156433498184710577783953474253149\
96221034888075845137057698397639931039296650460461211666513451311495\
13657400869056334867859885025601787284982567787314407216524272262997\
31979156860362940662474010148269755953315573665880056292127468065728\
52015704019406922855578006114290557553245497940089398491468126398607\
50085263298820224719585505344773711590656682821041417265040658600683\
84494510435499881288680131655155171467338832334085176381971359131237\
25486737347835373163415173693875652128997265979649032412087273486906\
99802996369265070088758384854547542272771024255049902319275830918157\
44820519642107283720493729351617534195777542245315244228039137240771\
78916612030610402558300550338867900521160254087404546209383843676378\
86658769912790922323717371343176067483352513629123362885893627132294\
18356588401041872786935443907708527828855830842709046107501900718493\
31399155582127523923298797806496390753338457191738228405018695704636\
26600235265587502335595489311637509380219119860471335771652403999403\
29636024557725796367328665434895732574099971056713162327234576676193\
76514081039991936339082864205100985774545240681068973924931382873622\
26257920000000000000000000000000000000000000000000000000000000000000\
00000000000000000000000000000000000000000000000000000000000000000000\
00000000000000000000000000000000000000000000000000000000000000000000\
00000000000000000000000000000000000000000000000000000000When the wheels are knownLike during World War II the Allied get hold of the Wheels for the Enigma and only had to find the order of the Wheels and the startposiotion of each installed wheel. So with the 8 bit Enigma engine with three wheels installed. There are 10 known wheels in the example below. <notice>/* Total number of wheels possible */
wheelstotal=10
/* With three wheels installed there would be 10*9*8 ways configure */
wheelcombinations=10*9*8
/* Each wheel can start in 256 ways */
notches=256*256*256
/* Total number of keys, when the wheels are known */
wheelstotal*wheelcombinations*notches</notice>
120795955200 |